VoroCrust
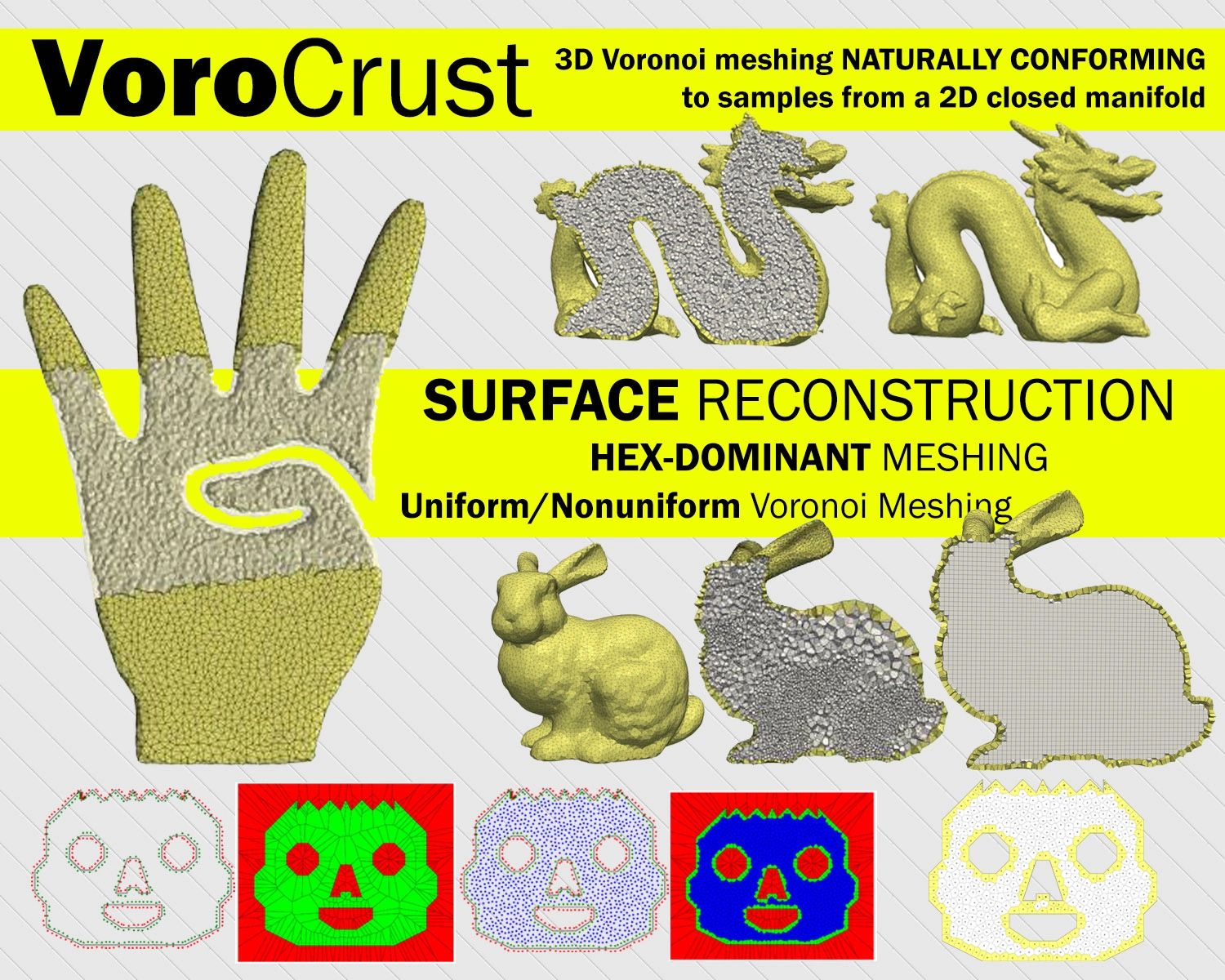
VoroCrust is the first correct algorithm for conforming Voronoi meshing of non-convex and non-manifold domains with guarantees on the quality of both surface and volume elements.

Polyhedral Meshing
Polyhedral meshes are increasingly becoming an attractive option with particular advantages over traditional meshes for certain applications. What has been missing is a robust polyhedral meshing algorithm that can handle broad classes of domains exhibiting arbitrary curved boundaries and sharp features. In addition, the power of primal-dual mesh pairs, exemplified by Voronoi-Delaunay meshes, has been recognized as an important ingredient in numerous formulations. VoroCrust is the first provably correct algorithm for conforming Voronoi meshing of non-convex and non-manifold domains with guarantees on the quality of both surface and volume elements. A robust refinement process estimates a suitable sizing field that enables the careful placement of Voronoi seeds across the surface circumventing the need for clipping and avoiding its many drawbacks. The algorithm has the flexibility of filling the interior by either structured or random samples, while all sharp features are preserved in the output mesh. We demonstrate the capabilities of the algorithm on a variety of models and compare against state-of-the-art polyhedral meshing methods based on clipped Voronoi cells establishing the clear advantage of VoroCrust output.
VoroCrust has attracted the attention of Earth Scientists at Sandia and Los Alamos National Laboratories due to its unique capabilities. The LANL Spent Fuel and Waste Science and Technology project webpage states: " Polyhedral meshing is important for flow and transport codes which include TOUGH2, FEHM, PFLOTRAN, and MODFLOW which are based on the two-point flux discretization. While the solution to flow/transport is stable without an orthogonal mesh, it is not accurate. Geometry conforming Voronoi tessellations are difficult to produce if the geometry is complex. So, if you want orthogonal discretization and you want complex geometry, you need conforming Voronoi tessellations. "
The VoroCrust software is owned by Sandia National Laboratories. To obtain the code, please send an email to msebeid@sandia.gov
VoroCrust Illustrated
This video illustrates the VoroCrust sampling conditions for smooth inputs. More details about the most recent variation of the algorithm which generates an automatic sizing functions and can handle sharp features and non-manifold domain can be found here.
An interview about VoroCrust by Sandia National Laboratories Intellectual Properties can be viewed here.
A recent article about VoroCrust in Sandia LabNews can be viewed here.
Photo Gallery
vorocrust in the news
Copyright © 2024 Mohamed S. Ebeida - All Rights Reserved.
Powered by GoDaddy Website Builder